Xavier Counasse, Chef du service Enquêtes, Le Soir en ligne du 29/10/2020 et Le Soir papier du 30/10/2020
Tout le monde en parle, mais personne (ou presque) ne la comprend. Alors pour pouvoir frimer en société, « Le Soir » vous donne quelques clés pour maîtriser la notion d’exponentielle, un incontournable de la crise covid.
Le mot est cuisiné à toutes les sauces depuis la découverte de la covid-19. On craint partout la « croissance exponentielle » de l’épidémie. Mais ce terme a beau sonner familièrement, il semble aussi mal compris. Quand le nombre de lits occupés dans les hôpitaux passe de 200 à 220 en une journée (+10 %), personne ne s’en inquiète. Un mois plus tard, quand il grimpe en 24 heures de 3.500 à 3.850 lits, ça commence à faire peur. Pourtant, dans l’intervalle, la croissance est restée la même : +10 % par jour. Silencieuse au début, l’exponentielle finit par exploser au visage. De quoi s’intéresser de plus près à ce concept mathématique. Le Soir vous le présente sous six facettes.
En une devinette
Un nénuphar double de surface chaque année. Et il lui faut 40 ans pour recouvrir toute la surface d’un étang. Question : combien de temps lui faudra-t-il pour en couvrir la moitié ?
Essayez cette petite devinette auprès de vos proches. Certains risquent de tomber dans le panneau, en répondant spontanément 20 ans. Mais la bonne réponse, c’est 39 ans. En effet, si le nénuphar occupe la moitié de la surface après 39 ans, et que sa taille double chaque année, il couvrira l’ensemble de l’étang l’année suivante, après 40 ans.
Ceci offre une très belle illustration de ce qu’est une exponentielle. La première année, le nénuphar est un petit point quasi invisible à l’échelle du lac. Après dix ans, ce nénuphar sera déjà 1.024 fois plus grand, mais restera toujours quasi invisible à l’échelle de l’étendue d’eau. Il lui faudra 35 années pour se faire remarquer, et occuper un peu plus de 3 % de la superficie du lac. Là, on pourrait penser qu’il n’y a rien qui presse, que l’étang n’est pas près d’être recouvert. Or il le sera 5 ans plus tard. C’est ça une exponentielle : un rythme de croissance continu (ici un doublement chaque année), avec une évolution qui semble lente au départ, mais qui, si elle perdure, peut devenir affolante.
En une légende
Un roi des Indes s’ennuyait. Il demanda qu’on invente un jeu pour le divertir. Un sage, dénommé Sissa, créa alors le jeu d’échecs. Enchanté, le roi promit à Sissa de lui offrir la récompense de son choix, aussi fastueuse soit-elle. Et Sissa demanda simplement à être payé en riz. Avec une règle assez simple : le Roi devait poser un grain de riz sur la première case de son jeu, deux sur la deuxième, quatre sur la troisième, et ainsi de suite en doublant chaque fois le nombre de grains. Jusqu’à ce que les 64 cases du jeu soient recouvertes. Mais le Roi ne parvint jamais à honorer sa promesse : il eut beau faire venir tous les sacs de riz du Royaume, et offrir à Sissa l’ensemble de ses réserves, le plateau ne fut jamais rempli.
Si le Roi avait révisé ses mathématiques, il ne se serait sans doute pas fait piéger. Même si le challenge a l’air simple, il se corse rapidement. Pour recouvrir la onzième case du jeu, il faut déjà placer 1.024 grains de riz. Pour la vingt-et-unième, plus d’un million de grains. Et pour la soixante-quatrième et dernière case, plus de 9 milliards de milliards de grains de riz. Certains scientifiques un peu allumés ont démontré que la production historique de riz ne permettait même pas d’honorer cette mission, et qu’il faudrait en produire durant 500 années supplémentaires pour espérer remplir l’échiquier. Sans parler de la faisabilité d’empiler plus de 9 milliards de milliards de grains sur une seule case.
En un virus
Imaginez qu’un homme soit atteint par un mystérieux virus, extrêmement contagieux. La seule chose que l’on sait sur lui, c’est que chaque personne qui en est porteuse va en contaminer trois autres. Après un premier cycle d’infections, le premier malade va donc en contaminer 3 autres. Puis ces 3-là vont en infecter 9, qui en toucheront 27, et ainsi de suite… A ce rythme-là, au 15ème cycle, plus de 20 millions de personnes auront déjà été infectées ! L’épidémie est donc rapidement hors de contrôle.
Mais en limitant les contacts entre humains, pour se protéger du virus, le taux de contamination change. Au lieu d’infecter 3 personnes, chaque malade ne transmet plus ce maudit virus qu’à 1,5 autre personne, en moyenne. Dans ce cas, après 15 cycles de contaminations, seuls 1.300 personnes seront contaminées. Et il faut 39 cycles pour franchir le cap des 20 millions d’infectés. Dans ces deux exemples, on est face à une croissance exponentielle. Toutefois, la première laisse beaucoup moins de temps pour agir avant l’envolée des cas que la seconde. C’est tout l’enjeu de la lutte actuelle contre le coronavirus : réduire au maximum ce facteur de contamination grâce aux mesures de distanciation, au masque… pour éviter de perdre définitivement le contrôle.
En économie
(Par Etienne de Callataÿ, économiste chargé de cours à l’UNamur)
Dans des circonstances exceptionnelles, le cerveau humain a tendance à anticiper ce qui va arriver par analogie, en se référant à une période passée qu’il juge comparable. Dans des circonstances normales, l’anticipation repose le plus souvent sur l’hypothèse d’une prolongation de la tendance récente. Si on demande de compléter la série 0-2-4, la majorité répondra 6, puis 8, procédant à ce qui est appelé une extrapolation linéaire : à chaque fois, on ajoute la même quantité, ici 2 unités. Si nous sommes habitués à procéder de la sorte, nous avons en revanche beaucoup plus de mal à nous figurer ce que peut être une extrapolation exponentielle, où après être passé de 2 à 4, on irait à 8, puis à 16.
Pourtant, en économie, les évolutions non linéaires sont omniprésentes. C’est notamment le cas en finances publiques, lorsque l’on parle de l’effet boule de neige : sous certaines circonstances, les charges d’intérêt sur la dette publique conduisent à un tel déficit qui gonfle la dette publique, ce qui, à son tour, alourdit les charges d’intérêt, et ainsi de suite avec, potentiellement à la clef, un phénomène « explosif ». C’est aussi le cas sur les marchés financiers, avec la règle dite des intérêts composés qui veut que les intérêts sur un capital génèrent à leur tour des intérêts. Supposons un taux d’intérêt de 10 % (certes, on est loin du compte aujourd’hui). Un capital de départ de 1000, devenu 1100 après 1 an, ne se transforme pas en 1200 après 2 ans mais en 1210. Et après 3 ans, ce n’est pas 1300 mais 1331. Et près de 2000 après 7 ans, là où on aurait pu penser que cela n’allait être que 1700.
Les petits font des petits, voilà ce qui se cache derrière une évolution exponentielle, en positif comme en négatif, en accumulation du capital comme en creusement d’une dette… ou en contamination d’une population.
En français
(Par Michel Francard, professeur ordinaire à l’UCL)
Au commencement était le verbe latin exponere « présenter, exposer », dont le participe présent est exponens « exposant ». De savants mathématiciens du 18e siècle vont créer, à partir de cette forme, le non moins savant adjectif exponentialis, adapté en exponentiel pour le commun des mortels. Avec la signification : « qui a trait à l’utilisation d’exposant ».
De là est issu fonction exponentielle – ou exponentielle –, pour désigner une fonction mathématique dont l’exposant est variable ou inconnu. Ce type de fonction permet de modéliser des phénomènes à croissance exponentielle. Si la fonction exponentielle n’est pas tombée de la dernière covid, la pandémie lui assure un taux de pénétration… exponentiel dans le grand public. Et dire que mon professeur de mathématique fait le masque !
En maths pures et dures
(Par Benoît Jadin, membre du Groupe d’enseignement mathématique (Gem))
On observe la croissance d’une population de bactéries in vitro, du type escherichia coli par exemple. Au temps initial, on en dénombre un million et on constate que ce nombre triple toutes les heures. C’est-à-dire 3 millions après une heure, 9 millions après deux heures, 27 millions après trois heures et ainsi de suite… Si on note t le temps en heures et N le nombre de bactéries en millions, on peut écrire que N(t)= 3 exposant (t).
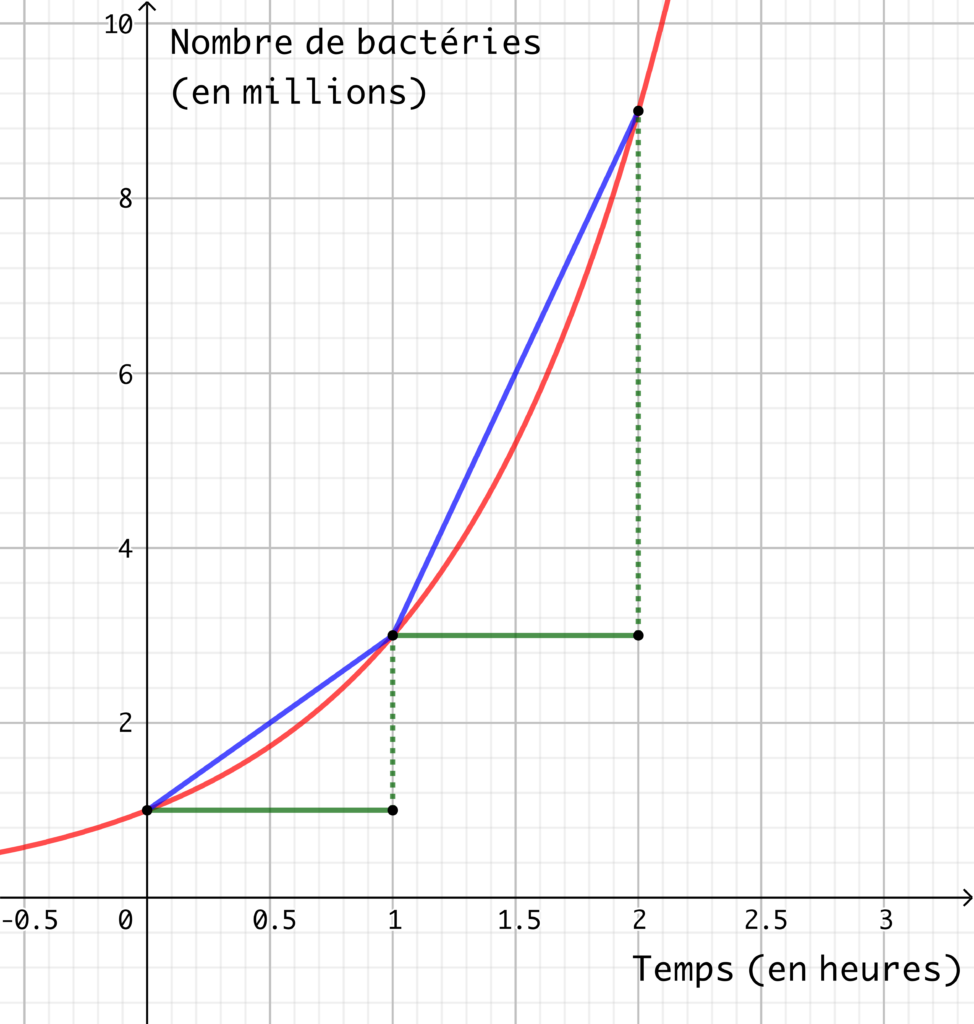
Mais après une demi-heure, combien y en a-t-il ? Si on suit un premier modèle de fonction en escalier (en vert sur la figure ci-dessus), rien ne bouge entre zéro et une heure mais la population triple d’un coup après une heure pile. Et c’est pareil après deux heures pile, puis trois heures… Ce modèle paraît peu vraisemblable.
Par contre si on considère un modèle « affin par morceaux » (en bleu sur le graphique), la croissance est linéaire durant la première heure, linéaire durant la seconde heure et ainsi de suite… Mais cette croissance varie d’heure en heure : 2 millions pour la première heure, 6 millions pour la deuxième heure, 18 millions pour la troisième heure. C’est bizarre et peu crédible que la croissance change d’heure en heure.
Finalement, considérons un modèle exponentiel (en rouge sur le graphique). Il se caractérise par le fait que pour deux périodes de temps égales, le facteur (multiplicatif) est le même. Entre le temps initial et une demi-heure, le nombre de bactéries a été multiplié par un coefficient a. Entre la demi-heure et l’heure, c’est le même facteur qui opère. Après une heure, on a donc N(t) = a.a. Mais, on sait aussi que la population triple en une heure ; il en résulte que a.a = 3 et que a = racinecarrée(3) .
Par convention d’écriture, la racine carrée d’un nombre est l’exposant « un demi » de ce nombre et on a donc N(1/2)=3exposant(1/2). Et après 20 minutes (soit le tiers d’une heure) : N(1⁄3) = 3exposant(1/3).
On peut se demander après combien de temps la population a doublé, c’est-à-dire ce que vaut t quand N(t) = 2, ou encore 3exposant(t) = 2. Pour trouver la solution de cette petite équation, on utilise la réciproque de l’exponentielle de base 3, à savoir le logarithme en base 3. On voit que c’est après un peu moins de 38 minutes que la population a doublé.
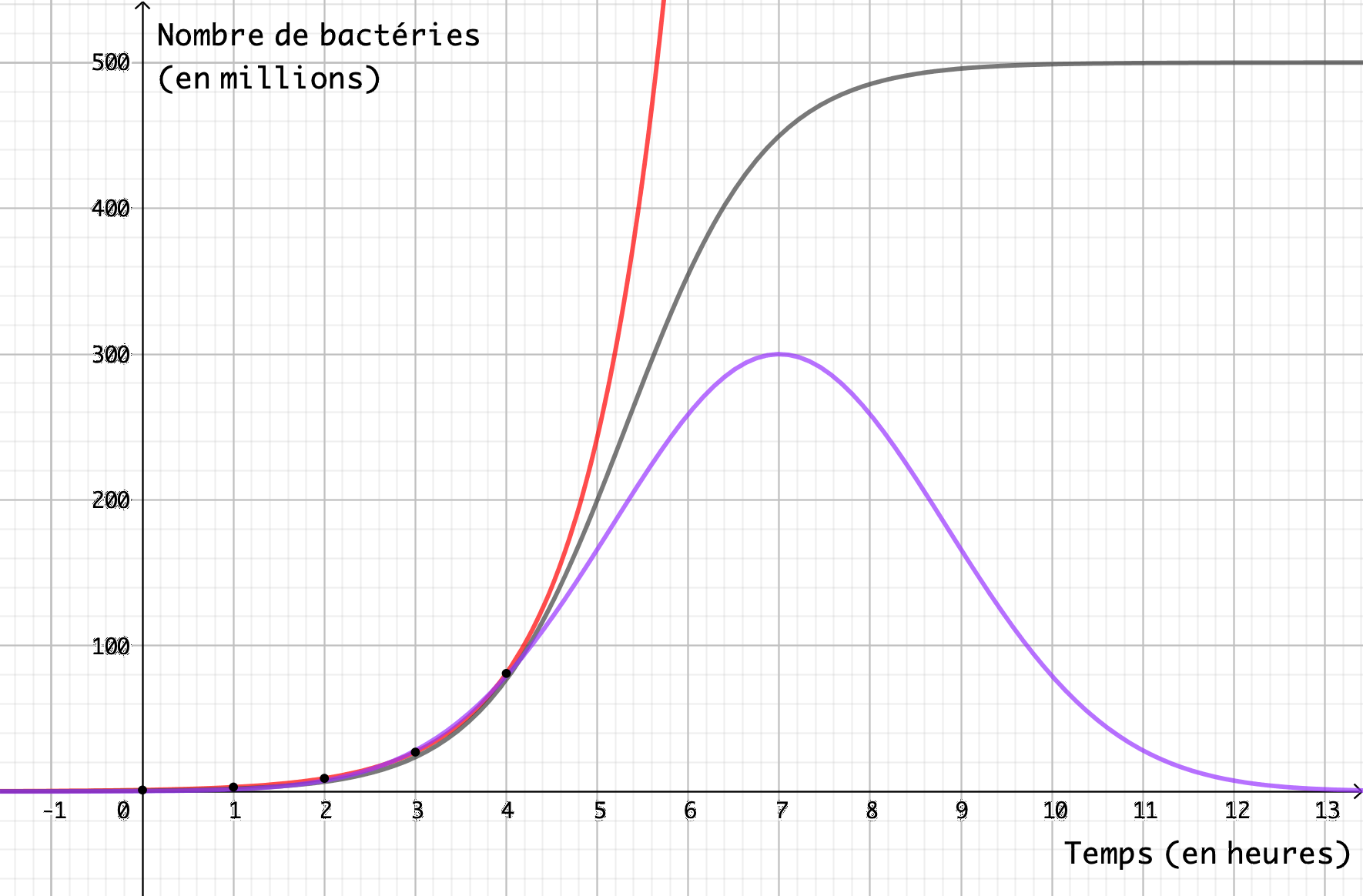
Que se passe-t-il au cours du temps ? La croissance exponentielle est relativement modérée au départ avant de s’emballer toujours plus, quand le temps avance. Est-ce possible ? Les bactéries ne peuvent proliférer sans énergie. Si les ressources sont renouvelées et limitées, le nombre de bactéries va plafonner après un certain temps et on observera plutôt une croissance comme celle qui est représentée en noir sur la figure ci-dessous.
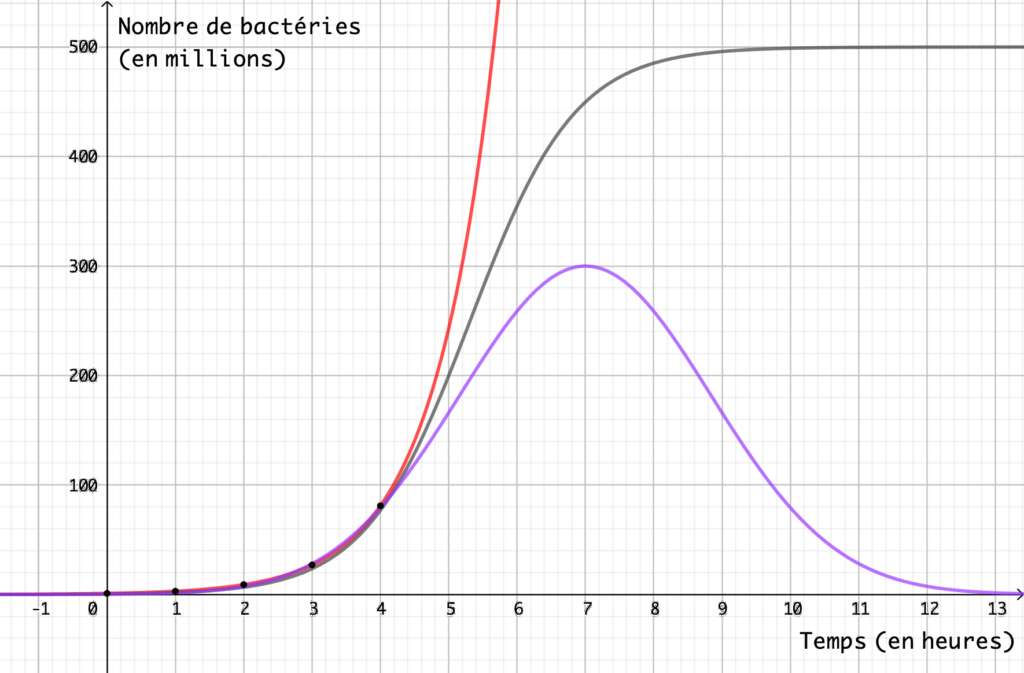
Et si les ressources ne se renouvellent pas, on va plutôt observer une régression du nombre et une courbe comme celle qui est représentée en fuchsia. Cela vous rappelle peut-être ce que vous avez observé comme évolution du nombre de personnes atteintes de la covid-19 lors de la première vague.
Notre système ne permettant pas d’afficher les symboles mathématiques de l’exposant et de la racine carrée sur l’ensemble des supports numériques, nous avons été contraints d’écrire cette opération en toutes lettres dans les formules ci-dessus. Nos excuses.



